Diffusion-Localization Transition Point of Gravity Type Transport Model on Regular Ring Lattices and Bethe Lattices

Abstract

Focusing on the diffusion-localization transition, we theoretically analyzed a nonlinear gravity-type transport model defined on networks called regular ring lattices, which have an intermediate structure between the complete graph and the simple ring. Exact eigenvalues were derived around steady states, and the values of the transition points were evaluated for the control parameter characterizing the nonlinearity. We also analyzed the case of the Bethe lattice (or Cayley tree) and found that the transition point is 1/2, which is the lowest value ever reported.

1 Introduction

Transport phenomena [1] have been recognized as one of the most important problems in many fields, including physics [2,3,4,5,6], biology [7,8,9], and social science and economics [10,11,12,13]. In particular, the gravity-type transport model has been widely applied in the fields of social science and economics to investigate phenomena such as world trade [10], human flow between cities [11], and firm-to-firm money transport [13]. One key feature of the gravity-type transport model is that the transport quantity depends on the power of the receiver’s quantity, where the power exponent may be nonzero. Typical cases, including those related to thermal and chemical transport, do not exhibit this dependency, whereas nonzero power exponents are observed in some cases in the fields of social science and economics [10, 14, 15]. In this study, we focus on the effect of the power exponent on the transport properties. We define a parameter $\gamma$ that controls transport nonlinearity. In a gravity-type transport system, larger quantities have a larger flow at positive $\gamma$ values. Owing to this property, a point with a large quantity may monopolize a large portion of the flows for some $\gamma$. We call this phenomenon the diffusion-localization transition and focus on estimating the critical value $\gamma _c$ at which the stable steady-state solution bifurcates. Although some graphs with no feedback loops have a large $\gamma _c$ that exceeds 1, some graphs have a transition point $\gamma _c$ less than or equal to 1. A previous study [16] reported that a complete graph has $\gamma _c = 1$, whereas a ring with infinitely many nodes has $\gamma _c = 1/2$. Table 1 summarizes the $\gamma _c$ of several synthetic graphs. This paper introduces regular ring lattices as a solvable network model and derives an exact formula for $\gamma _c$. We report the characterization of a structure with a low $\gamma _c$ in the context of the interaction length. We also consider the Bethe lattice as a typical graph to study mathematical models [17,18,19]. We analyze the system on the Bethe lattice both theoretically and numerically.

Table 1 List of diffusion-localization transition points $\gamma _c$ for known synthetic graphs

The remainder of this paper is organized as follows. Section 2 describes the gravity interaction model used in this study. We also provide fundamental tools as the basis for our analysis in Sect. 2. In Sect. 3, we present an analysis of the diffusion-localization transition point on regular ring lattices as a generalization of the results reviewed in Sect. 2. In Sect. 4, we present the second main result of the analysis of the transition point on the Bethe lattices and present the master equation as an analog of that in Sect. 2. Finally, we discuss the results and clarify the correspondence between our analysis and the dynamical phase transition of a biased random walk in Sect. 5.

2 Model and Review of Examples

In [13], a nonlinear relation for Japanese firm-to-firm transactions is found such that the annual trading volume $f_{ij}$ from a buyer firm i to a seller firm j is proportional to the powers of their annual sales $S_i$ and $S_j$, namely, $f_{ij} \propto S_i^\alpha S_j^\beta$ for some power exponents $\alpha >0$ and $\beta \ge 0$; in addition, $A=(A_{ij})$ is the adjacency matrix of the inter-firm network such that $A_{ij}=1$ if there exists an edge from node i to j, and $A_{ij}=0$ otherwise. In the examples of world trade [10] and human flow between cities [11], gravity model with distance dependency has been empirically confirmed. However, unlike in the cases of world trade and human flow, in the case of firm-to-firm transactions [13], distance dependency is very weak, i.e., $f_{ij}\propto (S_i^\alpha S_j^\beta )/(d_{ij}^\delta )$ with $\delta$ nearly equal to 0, where $d_{ij}$ is the physical distance between i and j. From this relation, the following mathematical model on a directed network of N nodes is named as a generalized gravity interaction model [16]:

$$\begin{aligned} \frac{d S_i^\alpha }{dt} \propto \sum _{k=1}^N \frac{A_{ki} S_i^\beta }{\sum _j A_{kj} S_j^\beta } S_k^\alpha - ( 1+\nu _i) S_i^\alpha + F_i, \end{aligned}$$

(1)

where $\alpha$ and $\beta$ are nonlinear power exponents, $A=(A_{ij})$ is the adjacency matrix of the given network, $\nu _i S_i^\alpha$ is the dissipation term that leaks out from the network, and $F_i$ is injected from outside the network. Here, t does not need to correspond to real time because we only need the stationary solution of Eq. (1), which is the realized S over the network. We assume that the network structure is fully described by its adjacency matrix $A_{ij}$, whose value is 1 if there is a directed link from i to j and 0 otherwise. $\beta =0$ corresponds to the equipartition where flow $f_{ij}$ does not depend on the sales of customer $S_j$, also known as PageRank, and $\beta =\infty$ corresponds to a monopoly, where $f_{ij}$ is equal to $S_i^\alpha$ for j of the largest sales $S_j$ and 0 for other neighborhood nodes. In this paper, we only consider the case where $F_i$ is independent of both i and t, namely $F_i=F$ for some constant F. For the stationary solution $S_i$ of Eq. (1) satisfies the following conservation law:

$$\begin{aligned} \sum _i S_i^\alpha = \frac{NF}{\nu }. \end{aligned}$$

(2)

We consider the following normalized quantity $x_i$ such that $x_i = S_i^\alpha /F$ for the remainder of this paper. The equation for $x_i$ is

$$\begin{aligned} \frac{dx_i}{dt} = \sum _{k=1}^N \frac{A_{ki}x_i^\gamma }{\sum _j A_{kj} x_j^\gamma } x_k - (1+\nu _i) x_i + 1, \end{aligned}$$

(3)

where $\gamma =\beta /\alpha$ for $\alpha$ and $\beta$ in Eq. (1). Hereafter, we set $\nu _i=\nu$ for all nodes i for simplicity. Thus, it is easy to confirm the following relation for the sum of the steady-state solution x from Eq. (2):

$$\begin{aligned} \sum _i x_i = \frac{N}{\nu }. \end{aligned}$$

(4)

In this model, the transport property is governed by the network structure $A=(A_{ij})$ and the nonlinear parameter $\gamma$. The formal statement of the diffusion-localization transition of this model is formulated as follows. There exists some $\gamma _c$ depending on the underlying network structure $A=(A_{ij})$ such that the steady-state solution of the model for $\gamma <\gamma _c$ bifurcates at $\gamma =\gamma _c$. In other words, $\gamma _c$ is the value of $\gamma$ at which the stable steady-state solution for $\gamma <\gamma _c$ becomes unstable. In this study, we used both theoretical tools and numerical simulations to study the transition point $\gamma _c$. We start the numerical calculation from the uniform state $1/\nu$ perturbed on one point to obtain a stationary solution when we perform numerical calculations. The perturbation will decay and diffuse over the system in the diffusion state, whereas the perturbation will grow in the localization state. For the diffusion state, we have the same stationary solution for different initial states, as far as we have performed the numerical calculation. For the numerical calculation, we determine the convergence by taking the $L^2$-norm of the relative increment as less than or equal to $10^{-6}$. We have confirmed that the absolute error of conservation law (4) is less than or equal to $10^{-2}$ under this convergence criterion.

Here, we review the previous results of the diffusion-localization transition on two illustrative examples of the ring and complete graphs. These two graphs have different transition points, $\frac{1}{2}$ and 1. The diffusion-localization transition point $\gamma _c$ on the two graphs is derived by considering the master equation of the linearized equation.

We define the following $N \times N$ weight matrix of transport $B=(B_{ki})$ of $\mathbf {x}=(x_1,\cdots ,x_N)^{\top }$ by

$$\begin{aligned} B_{ki}(\mathbf {x}) = \frac{A_{ki} x_i^\gamma }{\sum _j A_{kj} x_j^\gamma } = \frac{A_{ki}}{\sum _j A_{kj} \big (\frac{x_j}{x_i}\big )^\gamma } \end{aligned}$$

(5)

for $k,i=1,2,\cdots , N$. The denominator is the sum over the out-neighborhood j of node k(see Fig. 1). We calculate the perturbation response of B based on the perturbation $\mathbf {\delta x}$ from the stationary solution $\mathbf {x}$.

We consider cases in which a uniform steady-state solution is realized. When all node degrees are uniform, d, a uniform steady-state solution is realized by symmetry. In such cases, $B_{ij}=\frac{1}{d}$ for adjacent i and j. For the uniform steady-state solution $x_i = x \forall i$ over regular graphs, for a sufficiently small perturbation $\delta x$, the linear order of the perturbation response $\delta B_{ki}$ of the matrix element $B_{ki}$ in Eq. (5) is

$$\begin{aligned}&\delta B_{ki} = B_{ki}(\mathbf {x}+\mathbf {\delta x}) - B_{ki}(\mathbf {x}) = \frac{(x + \delta x_i)^\gamma }{\sum _{j} (x+\delta x_j)^\gamma } - \frac{1}{d} \nonumber \\&\quad = - \frac{\gamma }{d^2} \bigg [\sum _{j} \big (\frac{\delta x_j}{x} - \frac{\delta x_i}{x}\big ) \bigg ] + O(|\delta \mathbf {x}|^2) \end{aligned}$$

(6)

for $k,i=1,2,\cdots ,N$. The last term represents the second- or higher-order terms of $\delta \mathbf {x}$. $\sum _j$ represents the sum of the d neighborhood nodes of node k. Here, d is the coordination number; for example, d is $N-1$ for the case of a complete graph, and 2 for the case of a ring.

Thus, from the model equation

$$\begin{aligned} \frac{dx_i}{dt} = \sum _{k\ne i} \frac{x_i^\gamma }{\sum _{j\ne k} x_j^\gamma } x_k - (1+\nu ) x_i + 1 \end{aligned}$$

(7)

on the complete graph, the equation of perturbation is given by

$$\begin{aligned} \frac{d \delta x_i}{dt}&= \sum _{k\ne i} (B_{ki} \delta x_k + \delta B_{ki} x) - (1+\nu ) \delta x_i \nonumber \\&= \frac{1}{N-1} \bigg (\sum _{k \ne i} \delta x_k - (N-1) \delta x_i \bigg ) - \frac{\gamma }{(N-1)^2} \sum _{k \ne i } \bigg (\sum _{j \ne k} \delta x_j - \delta x_i \bigg ) - \nu \delta x_i \nonumber \\&=\big ( 1 - \gamma \frac{N-2}{N-1} \big ) \frac{1}{N-1} \bigg ( \sum _{k} \delta x_k - (N-1) \delta x_i \bigg ) - \bigg ( \gamma \frac{N-2}{N-1} + \nu \bigg ) \delta x_i. \end{aligned}$$

(8)

Thus, we can conclude that the transition point on the complete graph is 1 at $N\rightarrow \infty$ for the following reasons: in the region of $\gamma <1$, if $\delta x_i > \delta x_j \forall j\ne i$, then $\frac{d \delta x_i}{dt}<0$, which means that $\delta x_i$ decreases. On the other hand, in the region of $\gamma >1$, if $\delta x_i > \delta x_j \forall j\ne i$, then $\frac{d \delta x_i}{dt}>0$, which means that $\delta x_i$ increases. This picture can be confirmed in Fig. 1b by observing the variance of x over the average of x scaled by size N. In the case of the ring, we calculate the equation of perturbation $\delta x$ from a uniform steady-state solution as follows:

$$\begin{aligned} \frac{\delta x_r(t+\Delta t)-\delta x_r(t)}{\Delta t}&= \frac{1}{2 \Delta t} \bigg (\delta x_{r+\Delta r} - 2 \delta x_r + \delta x_{r-\Delta r}\bigg )\\&\quad - \frac{\gamma }{4 \Delta t} \bigg (\delta x_{r+2\Delta r} - 2\delta x_r + \delta x_{r-2\Delta r} \bigg ) - \nu \delta x_r. \end{aligned}$$

We set r as the Euclidean coordinate of nodes i and $r \pm \Delta r$ as the coordinate of the neighborhood of node i. Then, we have the following set of equations as a result of the continuum limit:

$$\begin{aligned} \frac{\partial \delta x}{\partial t}&= D(\gamma ) \frac{\partial ^2 \delta x}{\partial r^2} - \nu \delta x, \\ D(\gamma )&= \frac{\Delta r^2}{2\Delta t}(1-2\gamma ). \end{aligned}$$

(9a)

Here, we take the continuum limit of the equation to illustrate its relationship with the diffusion equation. From Eq. (9b), we find that the diffusion coefficient is positive for $\gamma <1/2$ and negative for $\gamma >1/2$. The first term, $\frac{\Delta r^2}{2\Delta t}$, in Eq. (9b) is the usual diffusion coefficient in one-dimensional space, and the second term, $-\gamma \frac{\Delta r^2}{\Delta t}$, is due to the nonlinearity of the interaction. This indicates that the diffusion-localization transition is caused by the two effects: diffusion in the usual sense determined by the network topology and the nonlinear effect of preferential flow towards nodes with larger x. Therefore, a phase transition between a normal diffusion phase and a localization phase occurs at $\gamma _c=1/2$. This diffusion equation establishes linearized gravity-type interactions as diffusion.

The diffusion-localization transition point $\gamma _c$ can also be calculated using a linear stability analysis. $\gamma _c$ in this sense is defined as $\gamma$, where the largest eigenvalue of the linearized matrix becomes positive. The general formula of the linearized matrix $J=(J_{ij})$ in Eq. (3) around x is given as follows:

$$\begin{aligned} J_{ij} = -(1+\nu ) \delta _{ij} + B_{ij} + \gamma \sum _k B_{ki}(\delta _{ij} - B_{kj})\frac{x_k}{x_i}. \end{aligned}$$

(9b)

We omit the argument x of B to simplify the notation. The term $\gamma \sum _k B_{ki} (\delta _{ij}-B_{kj}) \frac{x_k}{x_i}$ governs the effect of nonlinearity on the linear stability. Note that the sum of the row entries satisfies $\sum _j J_{ij} = -\nu$ for any x. Thus, J always has an eigenvalue $-\nu$ with the corresponding uniform eigenvector $(1,1,\cdots ,1)^{\top } \in \mathbb {R}^{N}$.

In the case of a complete graph, we have $B_{ij}=\frac{1}{N-1}$ for all $i \ne j$. Therefore,

$$\begin{aligned} J_{ij} = {\left\{ \begin{array}{ll} \frac{(N-2) \gamma }{N-1} - (1 + \nu ) &{} \qquad \text {if }\, i = j, \\ \frac{1}{N-1}-\frac{(N-2)\gamma }{(N-1)^2} &{} \qquad \text {if }\, i \ne j. \end{array}\right. } \end{aligned}$$

Thus, we obtain the exact eigenvalues of the linearized matrix given by

$$\begin{aligned} \lambda = {\left\{ \begin{array}{ll} -\nu , \\ \frac{N}{N-1} \bigg (\frac{N-2}{N-1}\gamma - 1 \bigg ) - \nu \qquad \text {with } N-1 \text { multiplicity}. \end{array}\right. } \end{aligned}$$

(10)

Hence, $\gamma _c$ for finite N and $\nu$ can be calculated as follows:

$$\begin{aligned} \gamma _c = \frac{N-1}{N-2} \bigg [ \big ( 1+\frac{N-1}{N} \big ) \nu \bigg ] \end{aligned}$$

(11)

Thus, at a large size limit $N\rightarrow \infty$ and zero dissipation limit $\nu \rightarrow 0$, $\gamma _c$ converges to 1.

On the other hand, in the case of the ring, we have $B_{ij}=\frac{1}{2}$ for $j=i \pm 1$. Thus, the linearized matrix is given by

$$\begin{aligned} J_{ij} = {\left\{ \begin{array}{ll} \frac{1}{2} \gamma - (1+\nu ) &{} \qquad \text {if }\, j=i, \\ \frac{1}{2} &{} \qquad \text {if }\, |j-i|=1, \\ - \frac{\gamma }{4} &{} \qquad \text {if }\, |j-i|=2, \\ 0 &{} \qquad \text {otherwise. } \end{array}\right. } \end{aligned}$$

Thus, the formula of the eigenvalues of circulant matrices [20] implies that

$$\begin{aligned} \lambda _l(\gamma ) = -\gamma \cos ^2 \bigg (\frac{2\pi l }{N}\bigg ) + \cos \bigg (\frac{2\pi l}{N} \bigg ) + \gamma -(1+\nu ) \end{aligned}$$

(12)

for $l=0,1,2,\cdots ,N-1$, depending on $\gamma$. $\gamma _c$ is the infimal value of $\gamma$ such that $\max _l \lambda _l(\gamma )>0$ by definition. Hence, $\gamma _c$ for the finite N and $\nu$ is

$$\begin{aligned} \gamma _{c}=\min _{j}\left( \frac{1}{2 \cos ^{2}\left( \frac{\pi j}{N}\right) }+\frac{\nu }{\sin ^{2}\left( \frac{2 \pi j}{N}\right) }\right) = \min _{j\ne 0} \left( \frac{1}{2 \cos ^2 \left( \frac{\pi }{N} \right) } +\frac{\nu }{\sin ^{2}\left( \frac{2 \pi j}{N}\right) }\right) . \end{aligned}$$

(13)

As $\nu \rightarrow 0$, we can neglect the term $\nu /\sin ^2(\frac{2 \pi j}{N})$ in Eq. (14). This allows us to minimize j to 1.

$$\begin{aligned} \gamma _{c} = \min _{j\ne 0} \left( \frac{1}{2 \cos ^2 \left( \frac{\pi j}{N} \right) } +\frac{\nu }{\sin ^{2}\left( \frac{2 \pi j}{N}\right) }\right) = \frac{1}{2 \cos ^2 \left( \frac{\pi }{N} \right) }. \end{aligned}$$

(14)

Therefore, we have $\gamma _c \rightarrow \frac{1}{2}$ at the large-size limit $N\rightarrow \infty$. The Taylor expansion yields an asymptotic, which is described as

$$\begin{aligned} \gamma _c - \frac{1}{2} \sim \frac{\pi ^2}{2} N^{-2}, \end{aligned}$$

(15)

where the symbol $\sim$ represents the major term in the limit of $N\rightarrow \infty$. Eq. (16) was confirmed numerically, as shown in Fig. 1c.

We confirmed that the diffused and localized solutions were stable. Figure 1d shows an example of diffused and localized solutions on the ring and their stability, starting from a uniform solution with perturbation on the origin. We obtained the uniform solution and localized solution on the ring for different $\gamma =0.000, 0.450, 0.518$. In Fig. 1e, we show the decay of the relative change of the $L^2$ norm of the solution $||x(t+1)||/||x(t)||$. We further numerically confirm that the largest eigenvalue of the linearized matrix at $\gamma > \gamma _c$ is negative.

Fig. 1

Gravity-type interaction and diffusion-localization transition. a Conceptual diagram of gravity-type weighted nonlinear transport. $B_{ki}$ is the weight of the transport from node k to node i. b Diffusion-localization transition over a complete graph with $\nu =10^{-4}$ for $N=25,50,100$, and 200. We calculate the steady solution starting from a uniform solution with perturbation on the origin. The x- and y- axes represent $\gamma$ and the variance of x over the average of x scaled by the system size N, respectively. The steady solution changes from the uniform steady-state solution for $\gamma <1$ to a localized solution for $\gamma >1$. As N increases, the transition point $\gamma _c$ decreases to a theoretical value of 1. c Numerically calculated transition points starting from a uniform initial state with perturbation on the origin over the ring and the asymptotic behavior described by Eq. (16) with $\nu =10^{-10}$. d Steady solutions over a ring with $\nu =10^{-10}$ for $N=50$ starting from a uniform steady solution with perturbation on the origin. e Convergence of point perturbation on the origin of the solution shown in Fig. 1d. Stability of the diffused solution and localized solution are illustrated. We measured the relative change of the $L^2$ norm $\frac{||x(t+1)||}{||x(t)||}$ as the measure of convergence where $x_i$ is the stationary solution

3 Analysis on Regular Ring Lattices

We consider regular ring lattices, as shown in Fig. 2a, as an example of the interpolation between the ring and the complete graph. The nodes are assumed to be arranged in a circle. Each node in this graph interacts with the 2k nearest neighbor. The model equation over a regular ring lattice is given by

$$\begin{aligned} \frac{dx_i}{dt} = \sum _{j; 0<|j-i|<k} \frac{x_i^\gamma }{\sum _{j'; 0<|j'-j|<k} x_{j'}^\gamma } x_{j} - (1+\nu ) x_i + 1. \end{aligned}$$

(16)

This equation includes the previous two examples, i.e., the ring for $k=1$, and the complete graph for $k=(N-1)/2$ as special cases. We have the exact eigenvalues of the linearized matrix on the uniform steady-state solution using the formula of the eigenvalues of the circulant matrices [20]. The linearized matrix of system (17) is derived as follows: The matrix element $J_{ij}$ depends only on the difference $m = |j-i|$. Therefore, we use both $J_m$ and $J_{ij}$ interchangeably.

$$\begin{aligned} J_{ij} = J_m = {\left\{ \begin{array}{ll} \gamma (1-\frac{1}{2k}) - (1+\nu ) &{} \text {if }\, m=0, \\ \frac{1}{2k} - \gamma \frac{2k-m-1}{(2k)^2} &{} \text {if }\, 1 \le m \le k, \\ -\gamma \frac{2k-m+1}{(2k)^2} &{} \text {if }\, k+1 \le m \le 2k, \\ 0 &{} \text {otherwise. } \end{array}\right. } \end{aligned}$$

(17)

Here, because $m=|j-i|$ represents the hopping distance from i to j, $1 \le m \le k$ and $k+1 \le m \le 2k$ corresponding to distances from nodes i to j are 1 and 2, respectively. To derive Eq. (18), we count the 2-hop paths from nodes i to j to evaluate the third term of Eq. (10). The number of 2-hop paths from i to j is determined by $m = |j-i|$ as $2k - m - 1$ for $1\le m \le k$, and $2k - m + 1$ for $k+1\le m \le 2k$. Thus, we obtain the linearized matrix as in Eq. (18).

Fig. 2

Regular ring lattice with 3 nearest neighbors. a Example of a regular ring lattice with $N=15$ nodes interacting with $2\times 3=6$ nearest neighbors. b Examples of counting 2-hop paths. In this case, the distance from i to j is one, the distance from k to l is two, the number of 2-hop paths from i to j is three, and the number of 2-hop paths from k to l is two. c Dependency of the transition point $\gamma _c$ of regular ring lattices on the interaction distance $\displaystyle \frac{N}{2k}$ with $\nu =10^{-10}$ for $N=100, 250, 500, 1000$ calculated using Eq. (19) by bisection method with tolerance $10^{-6}$. The rightmost figure corresponds to the ring, and the leftmost figure corresponds to the complete graph. Inset figure shows the empirical relation that $\gamma _c$ is approximated by $\frac{1}{2} \bigg [ 1+ \bigg (\frac{N}{2k}\bigg )^{-2} \bigg ]$

A linear stability analysis was performed using Eq. (17). The exact values of the N eigenvalues $\lambda _l$ for $l=0,\pm 1, \pm 2, \cdots$ are

$$\begin{aligned} \lambda _l(\gamma )= & {} \gamma \left( 1-\frac{1}{2k} \right) -(1+\nu ) + 2 \sum _{m=1}^{k} \bigg [\frac{1}{2k}- \gamma \frac{2k-m-1}{(2k)^2} \bigg ]\cos \big (\frac{2 \pi l}{N} m\big )\nonumber \\&- 2 \sum _{m=k+1}^{2k} \gamma \frac{2k-m+1}{(2k)^2} \cos \left( \frac{2 \pi l}{N} m \right) , \end{aligned}$$

(18)

depending on the value of $\gamma$. Note that $l=0$ corresponds to $\lambda _0 = -\nu$, which is the largest eigenvalue in the diffusion phase. From Eq. (19), $\gamma _c$ can be determined, as in the case of the ring. However, unlike in the case of the ring, we cannot theoretically determine l that maximizes $\lambda _l$ at $\gamma =\gamma _c$. Thus, we employ a bisection method that seeks the infimal value of $\gamma$ such that $\max _l \lambda _l(\gamma ) > 0$, where the tolerance of the bisection method is set to $10^{-6}$. We obtained the transition point $\gamma _c$, as shown in Fig. 2c. Figure 2c indicates that the transition point in the regular ring lattices continuously increases from ring ($k=1$), where $\gamma _c=1/2$ to complete graph($k=(N-1)/2$), where $\gamma _c=1$ as k increases, and it shows an empirical relation where $\gamma _c$ is approximated by $\displaystyle \frac{1}{2} \bigg [ 1+ \bigg (\frac{N}{2k}\bigg )^{-2} \bigg ].$ This result reveals that the proportion of interacting partners within the total nodes determines the transition point. Eq. (19) includes the special case of Eq. (13) of $k=1$.

The master equation is also calculated for a regular ring lattice. We use

$$\begin{aligned} \delta B_{ij} = B_{ij}(\mathbf {x}+\mathbf {\delta x}) - B_{ij}(\mathbf {x}) = -\frac{\gamma }{(2k)^2}\left( \sum _{l=1}^k \frac{\delta x_{i\pm l}}{x} - \frac{\delta x_j}{x} \right) \end{aligned}$$

(19)

to calculate the following two equations:

$$\begin{aligned} \frac{d \delta x_i}{dt}&= \sum _{m=1}^k ( B_{mi} \delta x_m + \delta B_{mi} x) - (1+\nu ) \delta x_i \nonumber \\&= \frac{1}{2k} \bigg ( \sum _{m=1}^k \delta x_m - 2k \delta x_i \bigg ) - \frac{\gamma }{(2k)^2} \sum _{m=1}^k \bigg ( \sum _{l=1}^k \delta x_{m \pm l} - \delta x_m \bigg ) - \nu \delta x_i. \end{aligned}$$

(20)

The master equation of perturbation (21) generalizes the two extreme cases of a complete graph and a ring. In the complete graph, the first and second terms of Eq. (21) can be combined such that

$$\begin{aligned} \frac{1}{2k} \bigg (\sum _{m} \delta x_m - 2k \delta x_i \bigg )&-\frac{\gamma }{(2k)^2} \sum _{m \ne i} \bigg (\sum _{m \ne l} \delta x_{m \pm l} - \delta x_m \bigg ) = \frac{1}{2k} \sum _{m \ne i} (\delta x_m - 2k \delta x_i)\\&- \frac{\gamma (2k-1)}{(2k)^2} \sum _{m \ne i} (\delta x_m - \delta x_i) \end{aligned}$$

Eq. (8) can then be recovered because $2k=N-1$ for a complete graph. The master equation of the ring can also be recovered from Eq. (21) by setting $k=1$.

4 Analysis on Bethe Lattice

To determine the behavior of model (3) on the Bethe lattice, we assume “isotropic x" for all points in the same layer to ease the computational cost. This assumption enables us to map the Bethe lattice to the corresponding one-dimensional (1D) chain consisting of “radial layers" by polarization(see Fig. 3). Following the mapping, the r-th$(r\ge 1)$ layer of the graph consists of $z(z-1)^{r-1}$ equivalent nodes.

Fig. 3

Isotropic assumption to simulate the gravity interaction model on the Bethe lattice. a Point of the r-th layer of the Bethe lattice of coordination number $z=3$. There is one adjacent point in the $(r-1)$-th layer and $(z-1)$ points in the $(r+1)$-th layer. b Schematic view of polarization mapping from the Bethe lattice to a 1D chain with a reflection barrier at the origin. The r-th layer consists of $z(z-1)^{r-1}$ points

Using this mapping, we obtain the following set of equations from Eq. (3) for each point in the r-th layer of the mapped chain:

$$\begin{aligned} \frac{dx_0}{dt}&= \frac{x_0^\gamma }{x_0^\gamma +(z-1)x_2^\gamma } z x_1 - (1+\nu ) x_0 + 1, \end{aligned}$$

(21)

$$\begin{aligned} \frac{dx_1}{dt}&= \frac{1}{z} x_0 + \frac{x_1^\gamma }{x_1^\gamma +(z-1)x_3^\gamma } (z-1) x_2 - (1+\nu ) x_1 + 1, \end{aligned}$$

(22a)

$$\begin{aligned} \frac{dx_r}{dt}&= \frac{x_r^\gamma }{x_{r-2}^\gamma +(z-1)x_r^\gamma } x_{r-1} + \frac{x_r^\gamma }{x_r^\gamma +(z-1)x_{r+2}^\gamma } (z-1) x_{r+1} - (1+\nu ) x_r + 1 \end{aligned}$$

(22b)

When we perform a numerical simulation, we set the free boundary condition for the two outermost layers, that is,

$$\begin{aligned} \frac{dx_{R-1}}{dt}&= \frac{x_{R-1}^\gamma }{x_{R-3}^\gamma +(z-1)x_{R-1}^\gamma } x_{R-2} + (z-1) x_R - (1+\nu ) x_{R-1} + 1, \end{aligned}$$

(22c)

$$\begin{aligned} \frac{dx_R}{dt}&= \frac{x_R^\gamma }{x_{R-2}^\gamma +(z-1)x_R^\gamma } x_{R-1} - (1+\nu ) x_R + 1. \end{aligned}$$

(23a)

The steady states of Eqs. (22) and (23) satisfy the following conservation condition:

$$\begin{aligned} \sum _i x_i = x_0 + \sum _{r=1}^R z(z-1)^{r-1}x_r = \frac{N}{ \nu }. \end{aligned}$$

(23b)

As an approximation, we consider the following homogeneous equation without the dissipation and injection terms:

$$\begin{aligned} x_r = \frac{x_r^\gamma }{(z-1)x_{r-2}^\gamma +x_r^\gamma } x_{r-1} + \frac{x_r^\gamma }{(z-1)x_r^\gamma +x_{r+2}^\gamma } x_{r+1}. \end{aligned}$$

(24)

Note that the uniform steady-state solution is one of the solutions to this equation. More importantly, however, the exponential solution $x_r \propto (z-1)^{-r}$ is another solution to Eq. (25).

Figure 4 shows an example of a steady-state solution for this equation. The steady-state solution of the model is almost uniform except in the neighborhood of the boundary layer for small $\gamma$, whereas an exponential-type steady-state solution is observed regardless of the system size for $\gamma$ close to $\frac{1}{2}$. The uniform steady-state solution is approximately achieved for $\gamma <\gamma _c$, except in the neighborhood of the boundary, while the exponential steady-state solution is approximately achieved near $\gamma _c$. For the numerical calculation, we determine the convergence by taking the $L^2$-norm of the relative increment as less than or equal to $10^{-6}$. We confirmed that the absolute error in Eq. (24) is less than or equal to $10^{-2}$ under the convergence criterion.

Fig. 4

Transition from the diffusion phase to the localization phase by increasing $\gamma$. The simulation was performed on the Bethe lattice with a coordination number $z=3$. Here, r in the two figures is the distance from the origin. For the numerical calculation, we determine the convergence by taking the $L^2$-norm of the relative increment as less than or equal to $10^{-6}$. We have confirmed that the absolute error of Eq. (24) is less than or equal to $10^{-2}$ under this convergence criterion. a Numerically calculated normalized steady-state solutions of Eqs. (22) and (23) for R=50, $\nu =10^{-4}$ for different $\gamma =0.000, 0.450, 0.503$ starting from the uniform solution with perturbation on the origin. The blue line indicates $\gamma =0$, the red line indicates $\gamma =0.45$, the purple line indicates $\gamma =0.503$, and the dashed black line indicates the exponential function $2^{-r}$ of the layer r. Here, we omit the value of the outermost boundary layer. The diffusion-localization transition near $\gamma$ close to 1/2 is clearly shown. b Exponential-type solution obtained at $\gamma _c=0.510$ with $\nu =10^{-4}$ for size $R=25,50,100,200$ starting from the uniform solution with perturbation on the origin. These solutions indicate the scale independence of the exponential solution near the transition point

We study the linearized equation of the model equation at a uniform steady-state solution with an infinite size limit. First, we sum up Eq. (22) for $\{x_r\}$ in the same layer r. Namely, for a set of the r-th layer points $S_r=\{ \text {point in the }r\text {-th layer}\}$, we define the total normalized quantity $X_r = \sum _{i; i\in S_r} x_i$. Then, we obtain the following equation of transport between adjacent layers from Eq. (22):

$$\begin{aligned} \frac{dX_0}{dt}&= \frac{ zX_0^\gamma }{zX_0^\gamma + (z-1)^{1-2\gamma } X_2^\gamma } X_1 - (1+\nu ) X_0 + 1, \end{aligned}$$

(25)

$$\begin{aligned} \frac{dX_1}{dt}&= X_0 + \frac{X_1^\gamma }{X_1^\gamma +(z-1)^{1-2\gamma }X_3^\gamma } X_2 - (1+\nu )X_1 + z, \end{aligned}$$

(26a)

$$\begin{aligned} \frac{dX_r}{dt}&= \frac{(z-1)X_r^\gamma }{(z-1)^{2\gamma }X_{r-2}^\gamma +(z-1)X_r^\gamma } X_{r-1} + \frac{X_r^\gamma }{X_r^\gamma +(z-1)^{1-2\gamma }X_{r+2}^\gamma } X_{r+1}\nonumber \\&\quad - (1+\nu ) X_r + z(z-1)^{r-1}. \end{aligned}$$

(26b)

At the large-size limit $R\rightarrow \infty$, a uniform steady-state solution is achieved because all the points of the graph become equivalent. Note that a uniform steady-state solution can be written as $X_r=z(z-1)^{r-1}x$ for $r\ge 1$ and $X_0=x$ for a constant $x=\frac{1}{\nu }$. To discuss the large-size limit, we introduce a unit time $\Delta t$ and lattice spacing $\Delta r$ such that the r-th layer points of the Bethe lattice are at distance $r \Delta r$. Then, we discretize Eq. (26c) as follows:

$$\begin{aligned} X_r(t+\Delta t) = F_r(X(t)), \end{aligned}$$

(26c)

where we define $F_r(X)$ by

$$\begin{aligned} F_r(X(t))= & {} \frac{(z-1)X_r(t)^\gamma }{(z-1)^{2\gamma }X_{r-2\Delta r}(t)^\gamma +(z-1)X_r(t)^\gamma } X_{r-\Delta r}(t) \nonumber \\&+\frac{X_r(t)^\gamma }{X_r(t)^\gamma +(z-1)^{1-2\gamma }X_{r+2\Delta r}(t)^\gamma } X_{r+\Delta r}(t) - \nu X_r(t) + z(z-1)^{r-1}. \end{aligned}$$

(27)

Then, the linearized equation of perturbation $\delta X$ from the uniform steady-state solution is denoted as

$$\begin{aligned} \delta X_r(t+\Delta t) = \sum _s \frac{\partial F_r}{\partial X_s}(X(t)) \delta X_s(t), \end{aligned}$$

(28)

where the sum over $s=0,\Delta r, 2\Delta r$, and $\cdots$. The nonzero elements of $\frac{\partial F_r}{\partial X_s}$ are computed as follows:

$$\begin{aligned} \frac{\partial F_r}{\partial X_{r-2\Delta r}}&= -\gamma \frac{(z-1)^2}{z^2}, \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial F_r}{\partial X_{r-\Delta r}}&= \frac{z-1}{z}, \end{aligned}$$

(30a)

$$\begin{aligned} \frac{\partial F_r}{\partial X_r}&= \gamma \frac{1}{z^2} \bigg (1 + (z-1)^2 \bigg ) -\nu , \end{aligned}$$

(30b)

$$\begin{aligned} \frac{\partial F_r}{\partial X_{r+\Delta r}}&= \frac{1}{z}, \end{aligned}$$

(30c)

$$\begin{aligned} \frac{\partial F_r}{\partial X_{r+2\Delta r}}&= -\gamma \frac{1}{z^2}. \end{aligned}$$

(30d)

We use Eq. (30) to linearize Eqs. (27) and (28). The resulting perturbation $\delta X$ for the uniform steady-state solution satisfies the following equation

$$\begin{aligned} \begin{aligned}&\frac{\delta X_r(t+\Delta t) - \delta X_r(t)}{\Delta t} = -\frac{z-2}{z} \frac{\Delta r}{\Delta t} \bigg [ \frac{\delta X_r - \delta X_{r-\Delta r}}{\Delta r} - 2\gamma \frac{\delta X_r - \delta X_{r-2\Delta r}}{2\Delta r} \bigg ] \\&+ \frac{\Delta r^2}{z \Delta t}\bigg [ \frac{\delta X_{r-\Delta r}-2\delta X_r + \delta X_{r+\Delta r}}{\Delta r^2} - \frac{2^2\gamma }{z} \frac{\delta X_{r-2\Delta r}-2\delta X_r + \delta X_{r+2\Delta r}}{(2\Delta r)^2} \bigg ] \nonumber \\&- \nu \delta X_r. \end{aligned} \end{aligned}$$

(30e)

When $z=2$, for a sufficiently small $\Delta r$ and $\Delta t$, we can approximate the differences in Eq. (31) by first- and second-order derivatives, which results in Eq. (9a). If the differences in Eq. (31) are approximated by a derivative for a sufficiently small but finite $\Delta t,\Delta r$, Eq. (31) can be formally rewritten as the following partial differential equation:

$$\begin{aligned} \frac{\partial \delta X}{\partial t}&= -\mu (\gamma ) \frac{\partial \delta X}{\partial r} + D(\gamma ) \frac{\partial ^2 \delta X}{\partial r^2} - \nu \delta X, \end{aligned}$$

(31a)

$$\begin{aligned} \mu (\gamma )&= \frac{z-2}{z}\frac{\Delta r}{\Delta t} (1-2\gamma ), \end{aligned}$$

(31b)

$$\begin{aligned} D(\gamma )&= \frac{1}{z} \frac{\Delta r^2}{\Delta t} \bigg ( 1-\frac{2^2 \gamma }{z} \bigg ), \end{aligned}$$

(31c)

where $\mu$ and D are the formal drift and diffusion coefficients, respectively. For a large coordination number limit $z\rightarrow \infty$, the diffusiveness will be lost, and the system behaves as a 1D system. By mapping the Bethe lattice to a 1D chain, diffusion from the origin in the original Bethe lattice is mapped to the drift in a 1D chain. The drift coefficient $\mu$ in Eq. (31b) is positive for $\gamma <1/2$ and negative for $\gamma >1/2$. The first term, $\frac{z-2}{z} \frac{\Delta r}{\Delta t}$, in Eq. (31b) is the net flow according to the gradient of $\delta X$ coming from one layer inward, and the second term, $-2\gamma \frac{z-2}{z} \frac{\Delta r}{\Delta t}$, is due to the nonlinearity of the interaction. Although the sign of $D(\gamma )$ in Eq. (31c) may change at $\gamma =\frac{z}{2^2}$, it is always larger than $\frac{1}{2}$ for $z\ge 3$. Therefore, localization is caused by changing the sign of the drift coefficient $\mu$ in Eq. (31b). The role of $\mu$ is dominant in describing the transitions. Hence, we can conclude that $\gamma _c = \frac{1}{2}$. The transition point is independent of the coordination number $z\ge 3$ of the Bethe lattice.

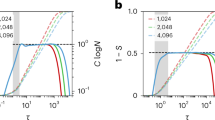
The dependency of the size on $\gamma _c$ is obtained by calculating the largest eigenvalues of the linearized matrix of Eqs. (22) and (23) for the numerically obtained steady solution of Eqs. (22) and (23) in Fig. 5 for the $z=3$ and $z=4$ cases. For the numerical calculation, we determine the convergence by taking the $L^2$-norm of the relative increment as less than or equal to $10^{-6}$. In each case, these figures show similar asymptotics of $\gamma _c - \frac{1}{2}$. Figure 5 implies that the asymptotics of $\gamma _c$ on the system size N are logarithmic. These simulation results confirm the independence of $\gamma _c=\frac{1}{2}$ on z.

Fig. 5

Asymptotics of transition point $\gamma _c$ toward $\frac{1}{2}$ for Bethe lattices with coordination number a $z=3$ and b$z=4$. The horizontal axis and vertical axis represent the reciprocal of the system radius R and $\gamma _c - \frac{1}{2}$ in logarithmic scales, respectively. Here, we use $\nu =10^{-4}$ and resolution $d\gamma =10^{-4}$ of $\gamma$ for both figures. Both $z=3$ and $z=4$ exhibit similar asymptotics. We obtain steady solution numerically starting from uniform state with perturbation on the origin. We note that transition points for each R did not depend on the initial state of numerical calculation of stationary solution

5 Discussion

In this paper, we review an analysis of the diffusion-localization transition on the complete graph and the ring as prototypes and confirm that the transition point $\gamma _c$ is 1 and 0.5, respectively, at the large limit.

Next, we generalize the results of the complete graph and the ring to the regular ring lattices by giving the general formula of the transition point $\gamma _c$ depending on the ratio of interacting pairs over the total number of nodes. We give a generalized eigenvalue formula of the linearized matrix, including the special cases of the complete graph and the ring, and show that regular ring lattices have transition points $\gamma _c$ between $\frac{1}{2}$ and 1, corresponding to the ring and the complete graph, respectively. A challenge in generalizing the diffusion coefficient of the ring is that there is no available method for measuring the effect of the aggregation process in the neighborhood on the diffusiveness at a given site. This problem is essential because the structural dependency of the transition point $\gamma _c$ may be determined by such an effect. We further relate theoretical critical points $\frac{1}{2}$ and 1 to the real-world example of firm-to-firm transactions reported in [16]. The transition point on firm-to-firm transactions is reported to be 0.9, between $\frac{1}{2}$ and 1. This suggests that the link density of the transaction network is between the ring and the complete graph. We found the regular ring lattices as a series of graphs with a transition point between 0.5 and 1; in particular, we can construct a graph on which the transition point is 0.9. One further topic is clarifying the difference between this example and the real transaction network.

Finally, we show that the nonlinear gravity-type transport model on the Bethe lattice has $\gamma _c=\frac{1}{2}$. By calculating the master equation and its drift coefficient of the linearized model, we argue that the diffusion-localization transition point $\gamma _c$ of the model at the large-size limit is $\frac{1}{2}$ in networks other than Euclidean lattices. In our analysis, the key point is to map the system to a 1D chain by polarization. The diffusion-localization transition on the Bethe lattice is understood by a sign change in the drift coefficient of the master equation. This result verifies a microscopic picture of the diffusion-localization transition that particles at the origin that has gone outside once will return again. Unlike spin systems [18] in which the transition points of the 1D chain and Bethe lattice are different, their transition points of them are the same for the system we analyzed. Bethe lattice shows different transition points from the mean field results. The relation between the mean-field behavior and the Bethe lattice is a further discussion point to be studied. The methodology of our analysis using polarization is quite similar to that of the analysis of a biased random walk on the Bethe lattice [21], which assumes a constant uniform central field toward the origin. The model of biased random walk over the Bethe lattice with coordination number z is described as follows: the probability of hopping toward the origin is $\frac{x}{z}$, where the bias parameter $0\le x\le z$ and the probability of hopping to go further is $\frac{z-x}{z}$. One difference between our model and the constant central field model is that our model does not directly assume a central bias toward the origin but assumes a localization parameter that conquers diffusiveness. The limitation of our approach is the assumption of polarization. The general formula of the transition point $\gamma _c$ on the regular ring lattices and Cayley trees based on linear stability analysis is still unknown. The behavior of the interaction length (see Fig. 2) and the asymptotic behavior of the transition point on the Bethe lattice (see Fig. 5) can be understood by finding such a formula to verify our numerical result in Fig. 2c of the regular ring lattices and the logarithmic convergence of the transition point of the Cayley trees to that of the Bethe lattice $\frac{1}{2}$.

To study the diffusion-localization phenomena in real-world complex networks, we also need to consider the direction of the edges of the graphs. Because nonlinear gravity interactions have been observed in many fields, the mathematical foundation of this model, especially of the nonlinear effect of transport over a complex network topology, is expected to be studied.